论文标题:Expected Returns in Treasury Bonds
中文标题:美国国债的预期收益
原文来源:Cieslak A, Povala P. 2015. "Expected Returns in Treasury Bonds. Review of Financial Studies", 28(10):2859-2901.
供稿:王宇新
封面图片来源:Pexels
编者按
文章研究美国国债的风险溢价,将国债收益率分解为通胀预期和特定期限利率周(cycles),变量cycle定义为与预期通胀率正交的收益率变化。短期cycle可以刻画真实的短期利率变化,与预期通胀一起,二者共同组成收益率曲线中的预期假说项(EH)。控制EH项后,文章从收益率曲线中提取出了测度风险溢价变化的变量。风险溢价因子可以预测样本内外的超额债券收益,文章还将得到的一般债券收益的预测因子归纳为远期利率的线性组合。
研究背景
Cochrane和Piazzesi(2005)证明了用远期利率的线性组合可以预测债券的超额收益率。在这篇文章中,作者证明了将周期因子加入超额收益率的预测中可以增强预测能力,该结果在样本内外均能预测超额收益率。
理论分析
文章将国债收益率分解为通胀预期和特定期限利率周期(cycles),变量cycle定义为与预期通胀率正交的收益率变化。短期cycle可以刻画真实的短期利率变化,与预期通胀一起,二者共同组成收益率曲线中的预期假说项(EH)。控制EH项后,文章从收益率曲线中提取出了测度风险溢价变化的变量。风险溢价因子可以预测样本内外的超额债券收益,文章还将得到的一般债券收益的预测因子归纳为远期利率的线性组合。
文章分解的经济基础是名义短期利率是一系列预期通货膨胀率和短期真实利率的和。作者注意到预期通货膨胀率处于持续变化之中,通常称之为趋势通货膨胀率,它和期限共同决定了长期利率水平(Kozicki,Tinsley,2001;Rudebusch,Wu,2008;Bekaert, Cho,Moreno,2010)。以过去的实际核心通货膨胀率反映趋势通货膨胀率,可以反映人们随着时间慢慢地改变通货膨胀率预期。文章证明了这一衡量可以很好地预测未来通货膨胀率,特别是在一年以内进行预测。相应地,周期(cycle)描述了短期利率围绕趋势通货膨胀率的均值反转,并且它和真实利率的波动相关。文章证明了cycle可以提前几年预测未来短期利率的变化。而无论是趋势通货膨胀率还是周期都没有预测债券超额收益率的能力,它们代表的只是独立于风险溢价关于短期利率期望的变量。
文章将名义收益率曲线中与趋势通胀正交的部分定义为:

表述为cycle,ct(n)的组成随期限而改变。文章结果表明趋势通货膨胀率可以解释收益率非条件方差85%的部分,决定了收益率的总体水平。cycle刻画了收益曲线斜率运动的60%。尽管cycle因子刻画了收益率方差的最小组成部分,但是它的影响会随着期限的引入而增加。趋势通货膨胀率,周期以及风险溢价这三个变量解释了不同期限收益率曲线方差的99%。然而,现代的利率期限结构模型将收益率曲线描述为三个组成部分--水平,斜度和曲率。文章将收益率曲线分解为三个部分--预期通货膨胀率、真实利率和风险溢价。文章目标是将收益率曲线分解为预期假说部分(预期通货膨胀率和真实利率)加上风险溢价部分。假设名义收益率受趋势通货膨胀率、真实利率和风险溢价这三个状态变量的主导。
研究设计
1.数据来源
文章使用从1971年11月到2011年12月美国联邦储备委员会H.15统计发布的月末不变期限国债(CMT)收益率,从中bootstrap出零息债券收益率曲线。CMT的数据分别包括6个月、1年、2年、3年、5年、7年、10年和20年的到期日,这使文章能够将长期到期日纳入分析。文章样本始于10年及以上期限的债券上市时。
通货膨胀数据来自FRED数据库。文章使用消费价格指数(CPI)通货膨胀(不受修订(Croushore和Stark ,1999),可视为实时数据)。为了说明公布滞后(给定月份的通货膨胀率在下一个月中旬公布),文章使用月底公开的消费物价指数数据。
2.主要变量
文章假设短期名义利率没有风险溢价,使用一个简单的趋势通货膨胀的衡量标准来确定影响短期利率的因素,构建了过去消费价格指数通胀率:

文章分析的主要部分使用核心CPI来构建τtCPI,因为核心通胀是债券投资者和货币政策制定者关注的衡量标准。图1将1年期和10年期收益率与τtCPI叠加,显示了τtCPI与利率的低频运动一致。图2表明τtCPI与联邦储备委员会的FRB/US模型的通胀预期一起移动。FRB/US模型中的期望值是从几个频率不规则的来源汇编的,需要插值到每月的频率。等式(2)的优点是简单,并且可以实时构建。
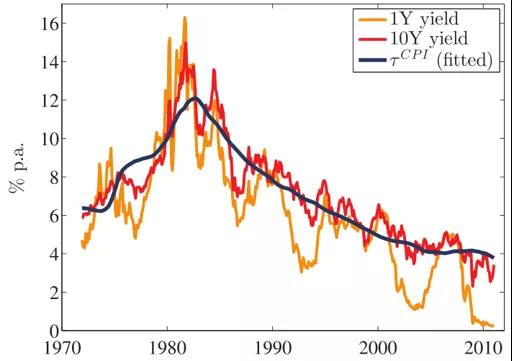
-图1- 收益率与趋势通胀率
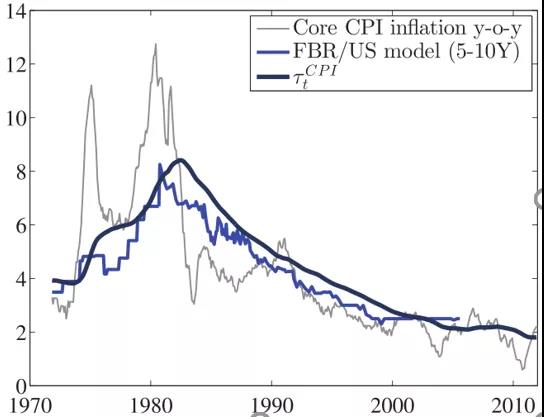
-图2- 核心CPI与长期通胀预期
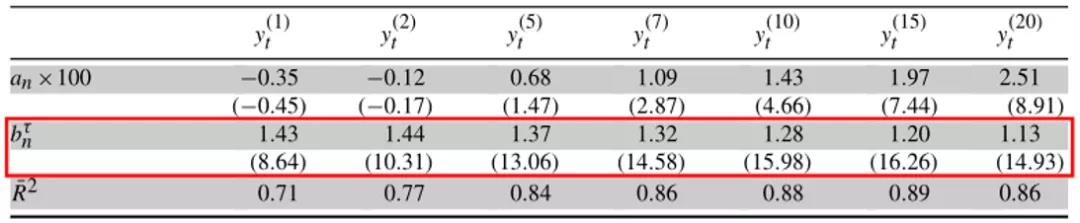
关于趋势通胀在收益率横截面中的作用,表1报告了根据τtCPI预测不同期限收益率的估计值:

单个变量解释了71%到89%的收益率差异,在长期限时,它的解释力更强。回归系数bnτ在1年期到期时为1.43 (t-stat=8.6),在20年期到期时为1.13 (t-stat=14.9),这表明了趋势通胀驱动收益率曲线的水平。
-表1- 收益率对τt CPI的回归
文章将回归(3)的残差定义为特定期限的周期,即给定期限的收益率中与趋势通胀正交的部分:

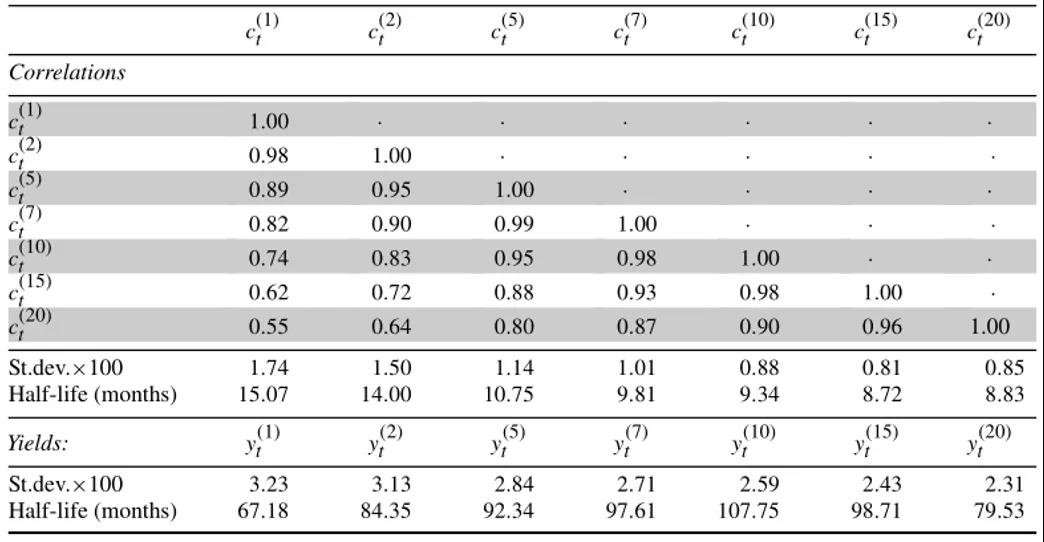
其中,ct(1)封装了第1节模型中真实因子的变化,称为“周期”,以表明它们不如收益率持久。表2总结了它们的特性。1年周期ct(1)的持久性最强,半衰期约为15个月,而10年周期ct(10)的半衰期不到一年。同时,收益率水平的半衰期都在5年以上。不同期限的周期之间的相关性相对较高,但不如收益率高。ct(1)和ct(20)之间的相关性最低,为0.55,而yt(1)和yt(20)之间的相关性为0.89。
-表2- 周期的特性
3.考虑小样本偏差
文章的实证依赖于债券超额收益的预测回归,关注1年持有期债券的超额收益。在预测回归中,文章使用每月重叠数据,并以年为单位测量时间。样本有470个月观测值组成:最后一个观测值是2011年12月实现的收益,用直到2010年12月观测的变量进行预测。文章取不同期限超额收益的平均值,用rxt+1表示。因为收益的波动性与债券期限成正比,文章将收益期限标准化,以避免过度加权特定期限。
回报的预测回归受到小样本偏差的困扰。文章从两个方面考虑这些偏差:
一方面,使用由Hodrick (1992)提出并由Wei和Wright (2013)扩展的反向回归的稳健标准误差。为了消除误差项的重叠,这种方法利用单周期收益的协方差和预测值的h周期和(对于月度数据和年度收益,h=12)。Ang和Bekaert (2007)表明,与常用的Hansen-Hodrick或Newey-West误差相比,反向回归标准误差具有更好的小样本性质,前两种误差都过度偏离了小样本中没有可预测性的零假设。
另一方面,由于高度持续的利率产生的偏差,基于回归的EH测试的预测R2被认为夸大了可预测性的真实程度(Bekaert,Hodrick和Marshall,1997)。因此,文章得到了在原EH下的R2分布的一个小样本(即其中真R2为零)。文章假设风险溢价为零,考虑了趋势通胀、实际因子的不同持续水平,校准各项参数,使用模拟数据对趋势通胀和实际因素的超额收益进行预测回归。在不同的参数配置中,来自这些回归的调整R2(R2)分布的第95个分位数在19%到23%的范围内。因此,即使在EH下,也可以期望获得有意义的预测R2。
实证分析
1.预测性回归
该节介绍债券超额收益的预测回归。文章使用平均回报rx t+1作为左侧变量,并在后续表格中报告特定到期日的结果。考虑多重收益率超额回报的标准预测回归(仅收益率回归):

将趋势通货膨胀的度量τtCPI加入仅收益率回归时,支持时变风险溢价的证据增强(收益率加τtCPI):

在使用多重收益率的回归中出现的问题是过度拟合和多重共线性。在表3的第(1)至(2)栏中,表示后者的系数共同具有很高的显著性,但单独不显著。然而,事实证明,可以简化回归(6)而不失去预测能力:

回归的全部预测内容来自收益率中与趋势通胀τtCPI正交的部分。故文章接着使用等式(4)中定义的周期预测回报:

-表3- 预测性回归结果
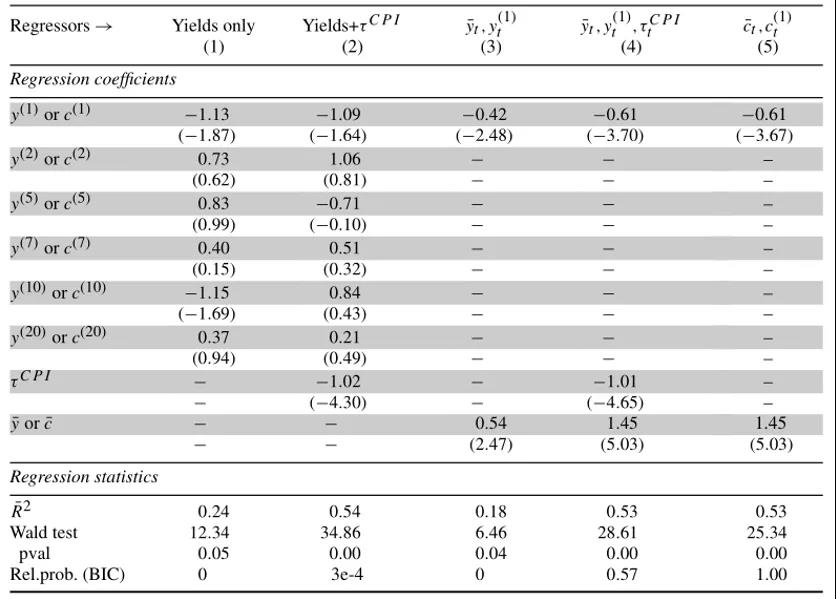
2. 趋势
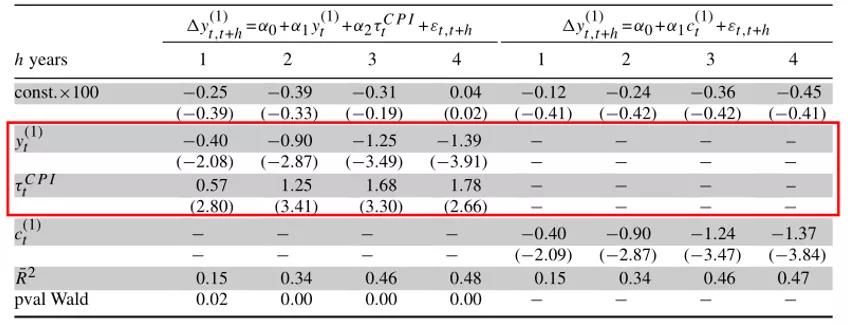
一个重要的问题是,如果使用过去利率的移动平均线(MA)而不是τtCPI来降低收益率,文章结果是否会出现。因此作者用平滑的过去利率(表示为τtyld)代替等式(7)中的τtCPI,用几个变量(1年期或5年期收益率)以及不同的平滑方法来构造τtyld,始终发现τtyld没有给回归增加预测内容,不能否认τtyld系数为零。这个结果扩展到将τtyld和τtCPI一起包含的情况。例如,使用1年期收益率的DMA作为τtyld,结果如下:
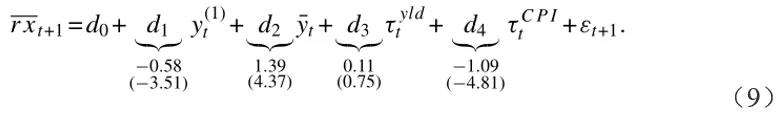
3.单一收益预测因子
Cochrane和Piazzesi (2005)表明,一个单一的预测因子,即在一组t期远期利率上预测rxt+1的拟合值,捕捉了不同期限的预期债券超额收益的变化。文章提出了一种构建单因子的替代方法,并标记为周期因子cft:

图3绘制了周期因子和平均周期ct,半衰期低于10个月(月AR(1)系数为0.925),cft比任何单个周期都不持久。
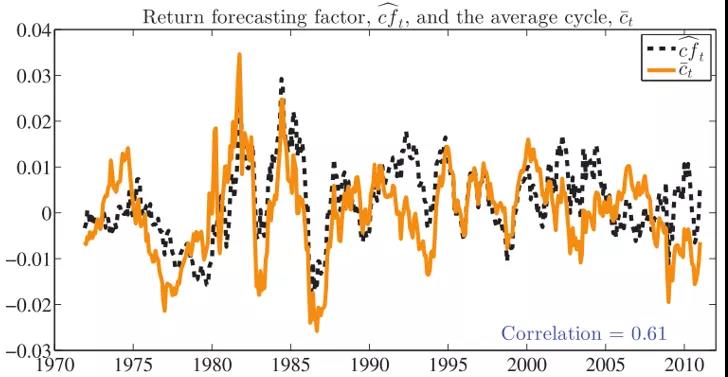
-图3- 回报预测因子cft和平均周期ct
文章对单个超额收益rxt+1(n)与周期因子进行回归。结果显示cft是不同期限的重要回报预测指标。因为人们可能会顾虑生成的回归量,作者bootstrap反向回归统计,并使用Li和Maddala (1997) bootstrap提供其分布的第5和第95个百分点。使用周期因子,与高度参数化的收益率加τtCPI回归(6)相比,预测内容基本上没有损失。rxt+1(n)对ct(1)和ct(n)的二元回归还表明,cft总结了收益率曲线中与特定期限周期相关的风险溢价信息。
4.结果解释
文章通过揭示三个正交因素的简单结构来描述收益率的横截面:趋势通胀τtCPI,一期周期ct(1),以及周期因子cft。文章表明趋势通货膨胀和一期周期在收益率中包含了EH项。
预测短期利率的变化。如果τtCPI和yt(1)捕捉到收益率曲线中的EH项,则应该可以预测未来的短期利率。表4和表5报告了对1年期收益率变化的预测。
-表4- Fama-Bliss (1987) 回归
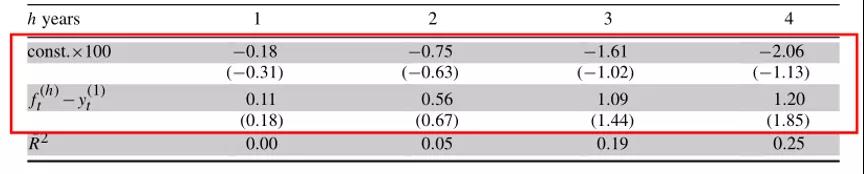
-表5- Fama (2006) 回归
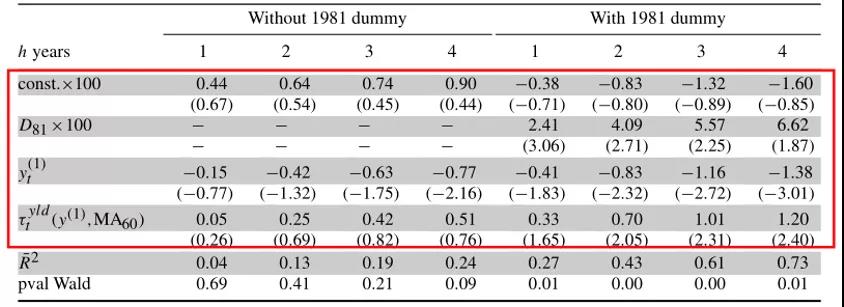
-表6- 趋势通货膨胀和1期周期
τtCPI将收益率的长期均值与趋势通胀联系起来。表(6)预测了τtCPI和yt(1)的短期变化。这些系数在所有层位都非常显著(p值不超过0.02)。结果与短期利率向缓慢移动的趋势通胀的均值回归一致,具有ct(1)的单变量回归与具有τtCPI和yt(1)的双变量规范具有基本相同的预测内容,这意味在与趋势通胀不相关的商业周期频率中预期短期利率存在显著的变化。总的来说,这些结果支持这样的解释,即τtCPI和ct(1)捕捉了收益率曲线的EH分量。
预测通货膨胀。文章结果表明,τtCPI变量在较长的期限(四个季度及以上)表现良好。对于较长的期限和所有项目的通货膨胀,τtCPI提供了所有竞争模型中最低的RMSE比率;对于核心通胀,τtCPI的表现与AORW相当。长期调查对核心通胀做出了更准确的预测,但在预测所有项目的通胀方面,它的表现不如τtCPI。
表7的面板B2显示了不同n的rx t+1(n)对ct(n)单变量回归的斜率系数和R2。未来回报周期的预测内容随着到期日的增加而增加,但可预测性明显弱于包含ct(1)和ct(n)的双变量回归(面板B1)。这是因为周期不仅包含期限溢价,还包含EH成分。文章已经证明,EH成分与溢价不相关。后者的相对重要性随着期限的增加而降低,这在增加的单变量回归中的R2可见一斑。然而,即使在长期限下,周期也不是风险溢价的直接衡量标准--这一事实表明了长期限下ct(1)的重要性。从经济解释的角度来看,人们会认为一个周期的周期ct(1)与事前实际利率挂钩。
-表7- 用周期因子预测收益
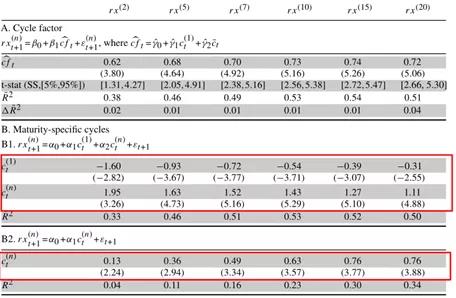
图4将ct(1)与两个事前实际利率指标叠加在一起,这两个指标是使用Livingston调查和专业预测者调查(SPF)的1年前预期通胀构建的。
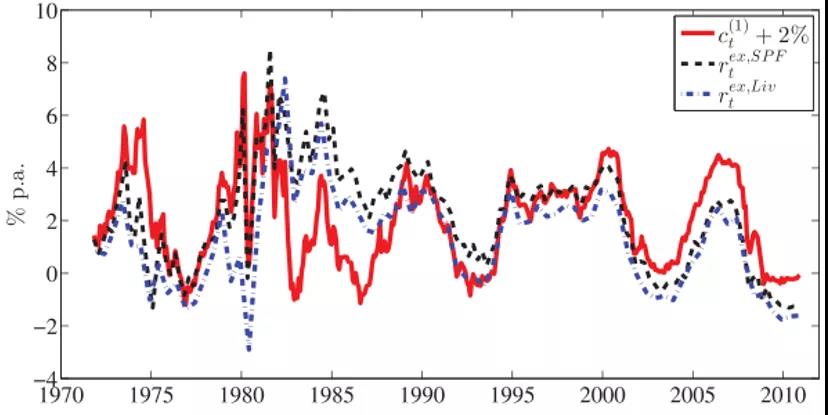
-图4- 一年期周期和事前实际利率
5.样本内外的Cycles和 CP因子
文章的可预测性结果自然导致了一个问题,即周期因子和Cochrane和Piazzesi (2005)的单一回报预测因子之间的联系。Cochrane和Piazzesi (2005)通过以下回归的拟合值构建了一个收益预测因子:
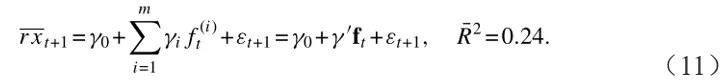
等式右边使用1年、2年、5年、7年、10年和20年的远期利率。回归结果表明使用其他到期日或更高的远期利率不会改变拟合。文章用CPt=γ,ft表示Cochrane-Piazzesi因子。为了研究文章结果和CP回归之间的联系,文章用τtCPI和正交残差c t(n)来表示n年期收益率:

根据τtCPI和cycles可以将CP因子γ,ft重写为:
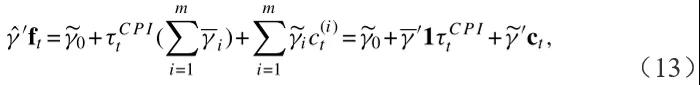
可以预期资本充足率主要反映收益率的变化,与趋势通胀无关。这可以通过在等式(13)中的每个项上用单独的系数允许超额收益负荷来测试:
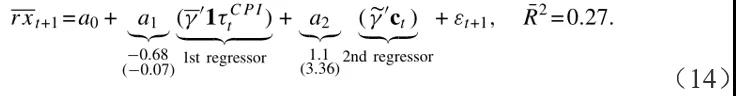
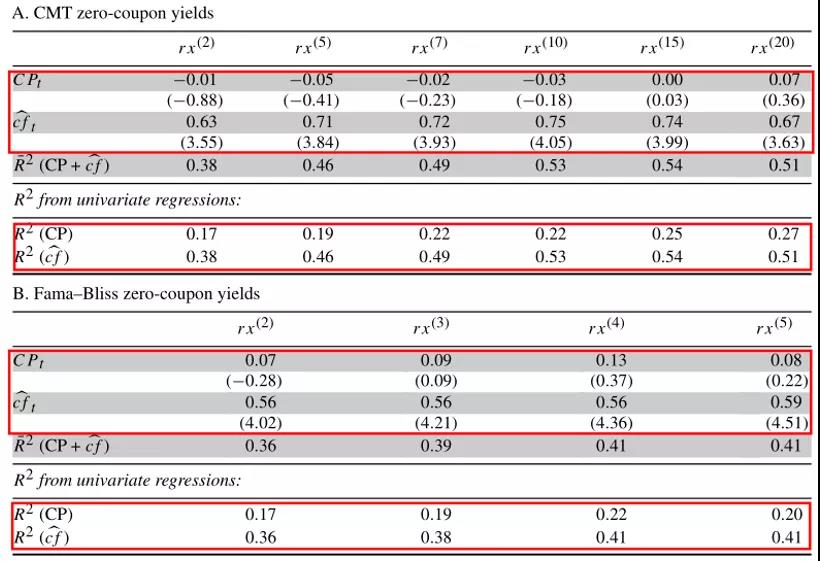
表8报告了双变量预测回归,其中包括周期因子cft和CP因子作为回归因子。有证据表明,CP回归对构建零息票收益率曲线的不同方法产生的测量误差非常敏感(Cochrane和Piazzesi,2008),因此文章提供了CMT以及Fama–Bliss数据集的估计值(当使用GSW收益率时,结论一致,文章未报告)。表中的主要观察结果是,CP因子在经济上和统计上变得无足轻重,并且没有超过cft的增量解释力。这一结论适用于所有债券到期日和两个数据集,并与这两个回报预测变量一致(两个变量捕捉了预期债券回报变化的共同来源),但CP因子噪音更多。
-表8- 使用CP因子和周期因子的二元预测回归
文章进行了样本外实验以评估预测随时间的稳定性。文章在1978年1月、1985年1月和1995年1月这三个日期开始样本外练习,这三个日期都在2011年12月结束,并考虑三组预测变量:周期、远期和远期现货价差。因为文章预测年度回报,所以对于每个样本,文章分别基于从1971年11月到1977年1月、1984年1月和1994年1月的期间获得初始参数估计。使用截止到t0的信息,文章预测t0+12个月的债券回报,并逐月扩展样本。文章样本外测试涉及以下三个统计数据:
(1)Clark和McCracken (2001)的包含检验(ENC-NEW):原假设是远期利率回归包含债券超额收益的所有可预测性,而这不能通过以趋势通胀为条件来进一步改善。
(2)远期利率与周期回归隐含的均方误差比(MSEs):小于1的数字表示周期产生的预测误差较低。
(3)Campbell和Thompson (2008)的样本外R2--R2 oos:将给定预测器对“naive”预测的预测性能与历史平均回报进行比较--正值表示预测模型的均方预测误差低于“naive”预测。
对于远期利率回归,文章使用期限为1年、2年、5年、7年、10年和20年的利率。对于周期回归,文章使用回归数不同的两个规格:(1)六个周期,到期日与远期利率相同;(2)两个周期,c(1)t和ct,用于构建cft。为了与远期利率回归进行比较,在ENC测试中,文章采用了六周期规范。最后,对于远期现货利差回归,文章用相应的远期现货利差f(n)t -y(1)t预测n年期债券的超额收益。结果表明预测在样本外依然稳定。
稳健性检验
文章稳健性检验包括三部分,第一部分首先讨论了基于调查通胀预期、当前已实现通胀以及平滑过去已实现通胀的不同方法的趋势通胀替代指标。在每种情况下,通过用一种替代的度量方法替换τt CPI来重构周期因子(cycle),并重新估计2年、5年和10年期限的收益率预测回归。其他期限的结论保持不变。
第二部分使用长期历史样本和短期调查数据进行稳健性检验。文章报告了追溯到1952年Fama–Bliss数据集开始时的结果,涵盖了美联储-财政部协议后的整个时期。作为趋势通货膨胀的衡量标准,文章使用了12个月前的中位数预测通货膨胀率(非合理调整),这是在整个样本中唯一的通货膨胀调查。文章根据Livingston调查以半年为频率进行回归 (每年6月和12月)。结果依然稳健。
第三部分使用来自调查(SPF和Blue Chip)的直接利率预测来比较调查隐含的预期收益与文章对风险溢价的衡量(周期因子)。
研究结论
文章建立了一个测度国库券超额收益率的方法,将收益率分解为预期部分和风险溢价部分。文章将不同期限的收益率分为两种效应:(1)由于预期通货膨胀率导致的收益率曲线的缓慢移动;(2)正交效应(针对不同期限持续性更弱的变量,文章定义为cycle)。文章实证证明,预期通货膨胀率和短期的cycle,可以被用于控制预期假说项,并且二者都不能预测未来收益率。短期的cycle与前期真实利率共同变化。期限较长时,cycle包含了短期利率预期和风险溢价,并且他们对债券收益率的预测能力随着期限的增加而增加。运用这个观察结果,作者建立了收益率预测因子--cycle因子,预测所有期限跨度内的超额收益率,既包含样本其外也包含样本期内,包括标准的债券预测因子,如期限利差或者远期利率的线性组合。
文章没有解决的问题是在国库券中决定风险溢价的经济因素。风险溢价较强的预测能力和快速的均值反转在标准的基于消费的资产定价模型框架内难以实现。文章的发现和文献中阐述的关于国库券风险溢价大部分变量和宏观变量以及标准风险测度是正交的结论是一致的。
Abstract
We study risk premium in U.S. Treasury bonds. We decompose Treasury yields into inflation expectations and maturity-specific interest-rate cycles, which we define as variation in yields orthogonal to expected inflation. The short-maturity cycle captures the real short-rate dynamics. Jointly with expected inflation, it comprises the expectations hypothesis(EH) term in the yield curve. Controlling for the EH term, we extract a measure of risk-premium variation from yields. The risk-premium factor forecasts excess bond returns in and out of sample and subsumes the common bond return predictor obtained as a linear combination of forward rates.
